Taehoon Kim (carpedm20)

http://neuralnetworksanddeeplearning.com/ 에 올라온 챕터을 이해하고 기록하고자 번역을 시작한다. 번역의 속도를 높이기 위해 수많은 의역이 포함되어 있다.

Info

원문:	http://neuralnetworksanddeeplearning.com/chap1.html
저자:	Michael Nielsen
역자:	김태훈 (carpedm20)

CHAPTER 1 Using neural nets to recognize handwritten digits

나는 인간의 사각계는 이 세계의 불가사의 중 하나라고 생각한다. 아래의 손글씨를 잠시 읽어보자.

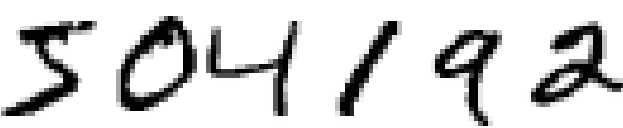
대부분의 사람들은 그다지 큰 노력없이 504192이라고 읽을 수 있을 것이다. 하지만 이러한 과정은 생각만큼 쉽지는 않다. 인간 좌뇌 우뇌에는 V1으로 알려진 일차 시각 피질(primary visual cortex)이 있으며, 이러한 V1은 1억 4천만개의 뉴런과 뉴런들 사이에 형성된 100억개의 연결(connection)들이 존재한다. 또한 다른 시각 피질(V2, V3, V4 그리고 V5)의 연결들은 더욱 복잡한 이미지 처리를 하게 된다. 즉, 우리의 머릿속에는 수억년동안 시각적 세계를 이해하기에 적합하도록 진화해온 슈퍼컴퓨터가 있다. 다시 손글씨 숫자들 이야기로 돌아가면, 숫자를 보고 인지하는것은 쉽지 않은 과정이다. 하지만, 우리는 두 눈이 보여주는 것을 꽤나 자연스럽게 이해해 왔다. 이러한 과정은 무의식 중에 일어나기 때문에 우리의 시각계가 얼마나 어려운 문제를 해결하는지 알아채지 못하곤 한다.

시각적 패턴 인지의 어려움은 위의 예시처럼 손으로 쓴 숫자들을 읽는 컴퓨터 프로그램을 만들려고 할 때 명백해 진다. 잠시만 생각해보면 우리가 쉽게 생각했던 것이 급격하게 어려워 보일것이다. 우리가 모양을 인지하는 과정을 간략하게 예를 들면 "9는 위쪽에 곡선이 있고 오른쪽 아래에는 수직선이 있다"가 될 수 있고 이것을 알고리즘(algorithm)으로 설명하기에는 쉽지가 않아 보인다. 당신이 그런 규칙들을 정확하게 만들려고 시도하다 보면 경고와 에러의 늪, 그리고 수많은 예외적인 케이스 문제에 쉽게 빠져 버리고 말 것이다. 절망적이군..

Neural Network는 이러한 문제를 전혀 다른 방식으로 접근한다. 핵심은 training example이라 불리는 많은 양의 손글씨 숫자들을 가지고:

숫자를 인지하는 방법을 배워가는 하나의 시스템을 만드는 것이다. 즉, neural network는 주어진 예시들을 이용해 숫자 인지를 위한 규칙을 자동적으로 만들어 낸다. 또한, training example의 수를 늘림으로써 network는 손글씨에 대해 좀 더 배울 수 있고 시스템의 정확도를 높일 수 있다. 그래서 위에 제시된 100개의 예시 뿐만 아니라 수천 수만개의 training example을 사용한다면 더욱 좋은 손글씨 인지 시스템을 만들 수 있게 될 것이다.

이 챕터에서는 neural network를 사용해 손글씨 숫자를 인지하는 컴퓨터 프로그램을 만들게 된다. 프로그램은 74 줄 밖에 안되며, 특별한 neural network 라이브러리를 전혀 사용하지 않는다. 하지만 이 짧은 프로그램은 사람의 중재없이 96프로의 정확도를 보여준다. 그리고 이후의 챕터에서는 정확도를 99프로로 높이게 된다. 실제로 뛰어난 상업 neural network는 은행에서 수표를 읽거나 우체국에서 주소를 읽는데 사용이 된다.1

우리가 손글씨 인지에 집중하는 이유는 neural network의 전반적인 이해에 도움이 되는 훌륭한 문제이기 때문이다. 문제로써 가장 좋은 이유는 바로 우리의 도전의식을 북돋기 때문이다. 그리고 deep learning과 같이 더욱 발전된 기술들을 이해하는데 도움이 된다. 이 책의 후반부에는, 컴퓨터 비전, 음성 인식, 자연어 처리 등의 다양한 분야에서 이러한 아이디어가 어떻게 적용되는지를 공부하게 될 것이다.

만약 이 챕터의 목적이 단순히 손글씨 숫자를 인지하는 프로그램을 짜는것이라면, 이 챕터는 훨씬 짧았을 것이다! 하지만 perceptron과 sigmoid neuron과 같은 인공 뉴런과 neural network의 일반적인 러닝 알고리즘인 stochastic gradient descent와 같이 neural network의 핵심이 되는 아이디어들을 공부하게 될 것이다. 따라서 나는 왜 아이디어들이 그렇게 정의가 되었는지를 설명하고 여러분들이 neural network에 대한 직관을 형성하는데 집중할 것이다. 그렇기 때문에 단순한 매커니즘을 설명할 때 보다 더 많은 설명을 추가하게 되었지만 (역자는 고통 받는다...), 여러분들의 깊은 이해를 위해서는 꼭 필요한 것들이다. 이 챕터를 다 읽고 나면, deep learning은 무엇이고 왜 중요한지를 이해하기 위한 준비가 될 것이다.

Perceptrons

Neural Network란 무엇인가? 먼저 시작하기 전에, 나는 인공 뉴런(artificial neuron)의 한 종류인 Perceptron에 대해서 설명하고자 한다. Perceptron은 Warren McCulloch 와 Walter Pitts 의 초기 작업 에 영감을 받아 1950, 60년대에 과학자 Frank Rosenblatt 에 의해 개발 되었다. 하지만 최근에는 perceptron 보다는 다른 인공 뉴런 모델을 주로 사용한다. 이 책에서 뿐만 아니라 오늘날 사용되는 대부분의neural network는 sigmoid neuron을 주로 사용한다. 우리는 조만간 sigmoid neuron에 대해 자세히 다룰것이지만, sigmoid neuron이 왜 정의가 되었는지 이해하기 전에 perceptron에 대해서 먼저 이해해 보도록 하자.

그렇다면 perceptron은 어떻게 작동하는 것일까? 하나의 perceptron은 여러개의 binary input인 x1, x2 ...를 받으며, 하나의 binary output을 만들어 낸다:

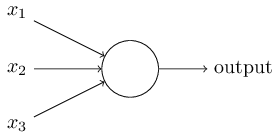
위의 예시에서는 x1, x2, x3를 input으로 받는다. 일반적인 경우, 이보다 더 많거나 적은 input들을 받을 수 있다. Rosenblatt은 output을 계산하는 하나의 공식을 제시했다. 그는 w1, w2.. 와 같이 각 input의 상대적 중요도를 나타내는 weight를 소개했다. 뉴런의 output인 0 또는 1은 각 weight와 input들의 곱의 합이 정해진 threshold 값 보다 크거나 작은지에 따라 결정된다. wieght와 같은 다른 parameter처럼 threshold는 실수값을 가진다. 이를 수식으로 설명하면:

\begin{eqnarray} \mbox{output} & = & \left\{ \begin{array}{ll} 0 & \mbox{if } \sum_j w_j x_j \leq \mbox{ threshold} \\ 1 & \mbox{if } \sum_j w_j x_j > \mbox{ threshold} \end{array} \right. \tag{1}\end{eqnarray}

이것이 perceptron이 작동하는 방법의 전부다!

Perceptron은 기본적은 수학 모델이다. Perceptron은 input의 중요도에 의해 결정되는 하나의 장치라고 생각할 수 있다. 이제 예를 하나 들어보자. 사실 현실적인 예는 아니지만, 여러분들이 perceptron을 이해하는데에는 도움을 줄 것이며, 추후에 좀 더 사실적인 예도 제시할 것이다. 먼저 주말이 오고 있고, 당신의 도시에 치즈 축제가 열린다고 가정해 보자. 당신은 치즈를 좋아하며, 축제에 갈것인지 안갈건지를 결정하려고 한다. 당신은 세가지 요소를 고려해 결정을 내리게 된다:

날씨가 좋은가?

당신의 남자친구 혹은 여자친구가 당신과 같이가려고 하는가?

축제가 대중 교통 근처에 있는가? (당신은 차를 가지고 있지 않다)

우리는 이 세가지 요소들을 x1, x2, x3 라고 표현할 것이다. 예를들어, x1 = 1은 날씨가 좋다는 뜻이며, w1 = 0은 나쁘다는 뜻이다. 비슷하게, x2 = 1이면 당신의 연인이 가고싶어 한다는 뜻이고, x2 = 0 이면 가기 싫어한다는 것이다. x3의 경우에도 마찬가지이다.

이제, 당신은 틀림없이 치즈를 좋아하고, 당신의 연인이 축제가 가기 싫어하더라도, 대중 교통 근처에 없더라도 기꺼이 축제에 가고싶다고 생각해보자. 하지만 아마 당신은 나쁜 날씨를 혐오하며, 날씨가 나쁜 경우 당신이 축제에 갈 방법이 없다고 생각해보자. 그러면 여러분은 perceptron을 사용해서 이러한 의사 결정 모델을 만들 수 있다. 한가지 방법은 w1 =6, w2 = 2, w3 = 2로 parameter를 설정하는 것이다. 다른 값들보다 더 큰 값을 가진 w1 이 날씨가 연인의 결정과 대중교통의 가까움 보다 훨씬 더 중요하다는 것을 나타낸다. 마지막으로, threshold 를 5로 정했다고 생각해 보자. 이러한 perceptron은 날씨가 좋다면 output은 항상 1이 되며, 날씨가 나쁘다면 항상 0이 된다. 즉, 연인의 결정과 대중교통의 가까움은 output에 전혀 영향을 끼지지 않는다는 것을 의미한다.

wieght와 threshold를 바꿔가면서, 우리는 다른 의사 결정 모델을 만들 수 있다. 예를들어, threshold 를 3으로 정했다고 가정해보자. 그렇다면 perceptron은 날씨가 좋을땐 언제든지 혹은 교통 수단과 연인의 의사 조건이 맞았을 때 축제에 참가할 수 있게 될 것이다. 이런 방법으로 전혀 다른 의사 결정 모델을 만들 수 있다. threshold 를 줄이는 것은 당신이 축제에 더욱 가고싶다는 의미를 나타낸다.

하지만 perceptron은 인간의 의사결정 모델과는 전혀 닮지 않았다! 하지만 위의 예시가 의미하는 바는 perceptron이 결정들을 만들기 위해서 어떻게 다른 요소들을 계산하는지를 보여준다. 또한, 복잡한 perceptron 네트워크를 구축한다면 미묘한 결정을 내릴 수 있게 될 것이다.

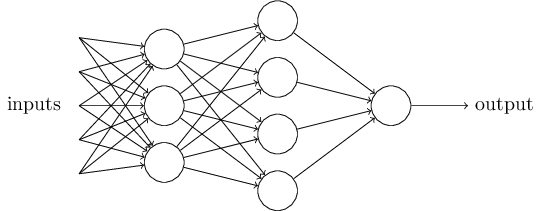
위에 보이는 네트워크에서는, 첫번째 열의 perceptron들이 input에 중요도를 계산해 3개의 간단한 결정을 내린다. 여기서 첫번째 열의 perceptron들을 첫번째 층(layer) perceptron 이라 부르겠다. 그렇다면 두번째 layer에 있는 perceptron들은 무엇을 하는가? 각각의 perceptron 은 첫번째 layer에서 만들어진 의사 결정들을 토대로 새로운 결정을 만들어 낸다. 이러한 방법으로 두번째 layer의 perceptron은 첫번째 layer보다 더욱 복잡하고 추상적인 레벨의 결정을 내릴 수 있다.마찬가지로 세번째 layer의 perceptron 은 더더욱 복잡한 결정을 내릴 것이다. 이러한 방식으로, multi-level layer의 perceptron 네트워크는 세련된 의사 결정을 내릴 수 있는 것이다.

그런데, 나는 perceptron을 하나의 output 만 만들어 내는 모델이라고 정의를 내렸다. 하지만 위의 네트워크는 여러개의 output 들을 만들어 내는 것 처럼 보인다. 사실, 그것들은 여전히 하나의 output 이다. 여러개의 output 화살표들은 단지 다른 perceptron에서의 output을 input으로 사용되는 것을 나타낼 때 유용할 뿐이다.

이제 perceptron 을 좀더 간단한 방법으로 정리해보자. $\sum_j w_j x_j > \mbox{threshold}$ 은 다소 다루기 어려운 식이며, 우리는 이것을 두개의 식으로 나눠 간단하게 할 수 있다. 가장 첫번째 변화는 $\sum_j w_j x_j$ 를 $w \cdot x \equiv \sum_j w_j x_j$ 처럼 하나의 점곱(dot product = scalar product)으로 바꾸는 것이다. 여기서 w 와 x 는 각각 weight 와 input 의 벡터가 된다. 두번째 변화는 threshold 항을 식의 반대쪽으로 옮기고, $b \equiv-\mbox{threshold}$ 로 나타낼 수 있다. 여기서 b는 bias의 약자이다.

\begin{eqnarray} \mbox{output} = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right. \tag{2}\end{eqnarray}

여기서 bias는 perceptron이 얼마나 쉽게 1의 output을 만드는지에 대한 척도라고 생각하면 된다. 큰 bias를 가진 perceptron은 쉽게 1이라는 output를 만들 수 있고, 매우 큰 음수의 bias의 경우에는 1의 output을 만들기 어려울 것이다. bias는 perceptron을 설명할 때 큰 비중을 차지하진 않지만 더욱 간단한 식을 만들 수 있게 해준다. 그렇기 때문에 앞으로는 threshold가 아닌 bias를 이용할 것이다.

나는 앞서 perceptron을 input의 중요도를 바탕으로 결정을 내리는 방법이라고 설명했다. 이러한 perceptron은 AND, OR, NAND와 같은 기본적인 논리 계산에도 사용될 수 있다. 예를 들어, 각각의 weight가 -2인 두 input을 가진 perceptron을 생각해 보자. 그리고 여기서 bias는 3이다.

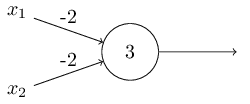
그러면 input이 00 일때 $(-2)*1+(-2)*1+3 = -1$ 의 결과가 양수이기 때문에 1의 output을 만든다. 01과 10의 input에 경우에도 output은 1이 된다. 하지만 11의 input에 대해서는 0의 output을 출력한다. 이는 $(-2)*1+(-2)*1+3 = -1$ 가 음수이기 때문이다. 그래서 우리는 perceptron을 이용해서 NAND 게이트를 만들었다!

NAND 게이트 예제는 perceptron을 간단한 논리 계산에 사용될 수 있음을 보여준다. 사실, 그 어따한 논리 계산도 perceptron으로 표현될 수 있다. 왜나하면 NAND 게이트로 어떠한 계산도 할 수 있기 때문이다.

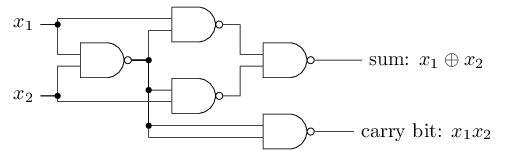
위와 같은 NAND 게이트를 perceptron으로 표현하기 위해선, 각 weight 가 -2이고 bias가 3인 perceptron을 사용하면 된다. 아래 그림은 완성된 network를 보여준다.

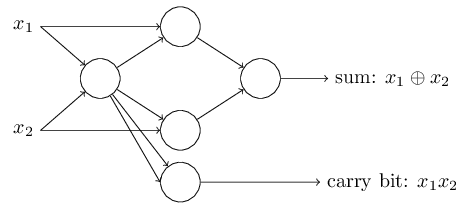
여기서 특이한 것은 가장 왼쪽에 있는 perceptron의 output이 가장 아래에 있는 perceptron의 input으로 두번 들어간다는 것이다. perceptron을 정의할때 나는 이러한 경우가 가능한지 그렇지 않은지에 대해 언급하지 않았다. 실제로 이것은 상관이 없다. 우리가 이러한 경우를 제거하고 싶다면, 두개의 선을 wiehgt가 -4인 연결로 합치면 된다. (만얀 이것이 잘 이해가 되지 않는다면, 여러분은 잠시 멈춰서 스스로 이해를 하는 시간을 꼭 가지도록 하자.) 아래의 그림은 weight가 표시되지 않은 선의 weight는 모두 -2이고 bias는 3인 perceptron으로 이루어진 네트워크를 보여준다:

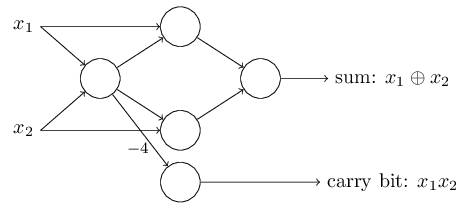
지금까지 나는 x1, x2와 같은 input을 perceptron왼쪽에 떠다니는 것으로 그려왔다. 하지만, input을 하나의 layer를 만들어 그리는 것이 더욱 평범한 방법이다:

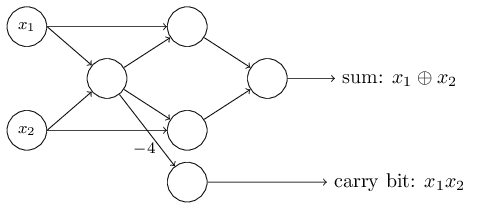
output은 있지만 input은 없는 input perceptron은

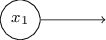
위와같이 간단하게 표기할 수 있다. 사실 이것은 input이 없는 perceptron을 뜻하지는 않는다. 한번 input이 없는 perceptron을 생각해 보자. 그렇다면 $\sum_j w_j x_j$ 은 언제나 0이 되며, $b > 0$라면 $1$의 output을 $b \leq 0$면 $0$의 output을 나타낼 것이다. 즉, perceptron은 우리가 원하는 값이 아닌 항상 고정된 값만 출력할 것이다. 그렇기 때문에 input perceptron을 perceptron이 아니라 단순히 x1, x2 ... 와 같은 고정된 값으로 정의된 단위 유닛(unit)으로 생각하는 것이 낫다.

위의 예제에서는 많은 NAND 게이트를 가진 회로를 perceptron의 network로 나타내는 방법을 보여주었다. 그리고 NAND 게이트로 모든 계산이 가능하기 때문에, perceptron의 network 또한 모든 계산이 가능하다는 것을 보여준다.

perceptron의 계산의 범용성(computational university)은 우리를 안심시키는 동시에 실망스러움을 안겨준다. 먼저 어느 컴퓨팅 장비에서도 perceptron network가 이용될 수 있기 때문에 안심이 된다. 허나 perceptron이 단지 새로운 형태의 NAND 게이트일 뿐이라고 생각한다면 다소 실망스럽다.

하지만, 인공 뉴런 네트워크의 weight와 bias를 자동적으로 조절(tuning)할 수 있는 러닝 알고리즘(learning algorithm)을 고안할 수 있기 때문에 그렇게 상황이 나쁜것은 아니다. 즉, 이러한 자동적 조절은 프로그래머의 직접적인 중재 없이도 외부적인 자극(output이 맞는지 맞지 않는지)에 반응한다는 말이다. 이러한 러닝 알고리즘은 전통적인 논리 게이트와는 철저하게 다른 방법으로 인공뉴런을 사용할 수 있게 한다. 때문에 논리 회로로 해결하기에는 극히 어려운 문제도 neural network를 사용하면 쉽게 해결할 수 있다.

Sigmoid neurons

러닝 알고리즘(Learning algorithm)이란 단어는 매우 멋져 보이지만, neural network에 어떻게 러닝 알고리즘을 적용할 수 있을까? 잠시 우리가 어떤 문제를 해결하기 위해 perceptron network를 이용한다고 생각해 보자. network의 input은 손글씨 숫자들을 스캔해서 얻은 픽셀 데이터라고 가정하자. 그리고 netowrk를 통해서 숫자를 제대로 구분하기 위해 올바른 wieght 와 bias를 찾고 싶다고 가정하자. 우리는 러닝이 어떻게 작동하는지 보기 위해, weight나 bias에 작은 변화를 주었다. 우리는 이러한 작은 변화가 network의 결과에 적당한 변화를 만드는 것을 확인하고 싶다. 잠시후 보게 되겠지만, 이러한 작은 변화는 러닝을 가능하게 한다. 이것이 우리가 원하는 network의 구조이다 (확실히 손글씨 인지를 하기에는 매우 간단하다):

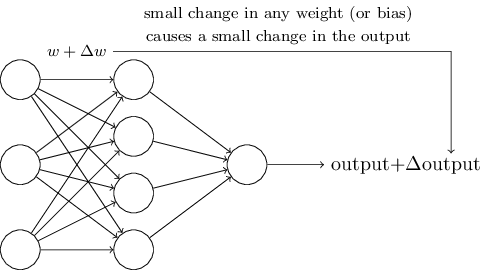
만약 weight나 bias의 작은 변화가 output에 작은 변화를 만든다면, 우리는 이 사실을 통해 network가 제대로 작동하도록 조정할 수 있을것이다. 예를 들어, network가 숫자 "9"를 "8"이라고 잘못 분류했다고 가정하자. 우리는 weight와 bias에 변화를 주면서 network가 이미지를 "9"라는 결과로 분류하도록 만들 수 있을것이다. 그리고 이러한 과정을 반복하면서 올바른 output을 만들어 내는 wieght와 bias를 찾게 된다. 바로 network가 러닝을 하는 것이다.

문제는 network에 perceptron이 있다면 이러한 과정이 이루어지지 않는다는 점이다. 사실 weight와 bias의 작은 변화는 network의 결과를 완전히 바꿔버리는(즉 0에서 1로 혹은 1에서 0으로) 결과를 초래할 수 있다. 이러한 변화는 network의 나머지 부분을 완전히 그리고 이해하기 복잡하게 바꿔버릴 수 있다. 그렇기 때문에 "9"라는 숫자가 제대로 분류가 되었다 하더라도, 다른 이미지를 인지하는 부분이 수정하기 까다롭게 바뀌어 버릴지도 모른다. 이렇기 때문에 점차적으로 weight와 bias를 변화해 가면서 우리가 원하는 행동을 만들어가는 것이 매우 어렵다. 하지만 이러한 문제를 해결하는 똑똑한 방법이 있을것이다.

여기서 우리는 sigmoid neuron이라 불리는 새로운 인공 뉴런(artificial neuron)을 소개함으로써 이 문제를 해결할 수 있다. sigmoid neuron은 perceptron과 비슷하지만, weight와 bias의 변화가 output에 단지 작은 변화만을 만들 수 있도록 개조되었다. 이것이 sigmoid neuron의 network가 배움을 가능하게 하는 중요한 사실이다.

자, 이제 sigmoid neuron에 대해 설명하겠다. 우리는 perceptron을 그린 방식으로 sigmoid neuron을 그릴 것이다:

perceptron의 경우와 같이, sigmoid neuron 또한 x1, x2 ... 와 같은 input이 있다. 하지만 0이나 1 뿐만이 아니라 0과 1사이의 값들을 input으로 받을 수 있다. 그래서 0.638 .. 과 같은 값이 sigmoid neuron의 input이 될 수 있다는 말이다. 또한 perceptron처럼 sigmoid neuron에는 w1, w2 ... 와 b 와 같은 wieght와 bias가 있다. 하지만 output은 0 혹은 1이 아닌 $\sigma(w \cdot x+b)$의 값을 가지며, 여기서 $\sigma$는 sigmoid function이라고 불린다. sigmoid function의 정의는 다음과 같다:

\begin{eqnarray} \sigma(z) \equiv \frac{1}{1+e^{-z}}. \tag{3}\end{eqnarray}

이 문장들을 좀더 깔끔하게 나타내면, input x1, x2 ...와 weight w1, w2 ..., 그리고 bais b를 가진 sigmoid neuron은 아래와 같다.

\begin{eqnarray} \frac{1}{1+\exp(-\sum_j w_j x_j-b)}. \tag{4}\end{eqnarray}

처음 위의 식을 보면 perceptron의 식과는 무척 달라 보일것이다. sigmoid function의 수식은 당신이 이미 친숙한 경우가 아니라면 접근하기 어려워 보일지도 모른다. 사실, perceptron과 sigmoid neuron 사이에는 공통점이 많이 있으며, sigmoid 함수의 대수적 형태가 perceptron 보다 더 기술적인 내용들을 포함하고 있다.

그렇다면 $\sigma$는 어떻게 생겼을까? 어떻게 우리는 그것을 이해하면 될까? 사실 $\sigma$의 정확한 형태보다는 함수를 그렸을 때의 모양이 더욱 중요하다. 아래 그림은 함수를 그래프로 그린 것이다:

아래의 그림은 sigmoid 함수가 평탄해진 계단 함수(step function)를 나타낸다:

만약 $\sigma$가 step function이었다면, sigmoid neuron은 perceptron과 같았을 것이다. 왜냐하면, $w \cdot x + b$가 양수인지 음수에 따라 sigmoid neuron의 output이 1 또는 0으로 결정이 되기 때문이다. 하지만 위의 그래프처럼 생긴 실제 $\sigma$ 함수를 사용하면서 평탄해진 perceptron이 된다. 따라서 구체적인 수식보다는 이러한 평탄함이 $\sigma$ 함수의 핵심이라고 볼 수 있다. $\sigma$의 평평함은 작은 $\Delta w_j$와 $\Delta b$가 neuron의 작은 $\Delta \mbox{output}$을 만든다는 것을 의미한다. 미적분을 계산하면, $\Delta \mbox{output}$는 대략적으로:

\begin{eqnarray} \Delta \mbox{output} \approx \sum_j \frac{\partial \, \mbox{output}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{output}}{\partial b} \Delta b, \tag{5}\end{eqnarray}

의 값을 가지게 된다. 당신이 도함수(partial derivatives)에 익숙하지 않다고 해서 불편함을 느낄 이유가 전혀 없다! 위의 수식이 복잡해 보이더라도, 매우 간단하다: $\Delta \mbox{output}$는 $\Delta w_j$와 $\Delta b$의 1차 함수로 표현할 수 있다는 말이다. 이러한 선형성은 output에서 발생하는 작은 변화가 우리가 원하는 방식으로 만들어 질 수 있도록 weight와 bias를 바꾸기 쉽다는 것을 의미한다. 그렇기 때문에 sigmoid neuron은 perceptron의 형태와 질적으로 많이 비슷하며, 어떻게 weight와 bias를 바꿀지를 알아내는 것이 훨씬 쉽다.

$\sigma$ 함수의 정확한 식이 아니라 그 모양이 훨씬 중요하다면, 왜 우리는 Equation (3)은 어떻게 나오게 된걸까? 사실 우리는 종종 활성화 함수(activation function) $f(\cdot)$에 대한 output이 $f(w \cdot x + b)$인 neuron을 종종 고려하게 될 것이다다. 우리가 다른 활성화 함수를 사용할때 가장 큰 변화는 Equation (5)의 특정 변수의 변화이다. 우리가 $\sigma$함수를 이용해서 이러한 도함수를 계산하게 될 때 지수함수의 특별한 성질 때문에 계산이 매우 간단하게 된다. 다시 정리하자면, $\sigma$함수는 neural network에서 보편적으로 쓰이며, 이 책에서 가장 많이 사용될 활성화 함수다.

그렇다면 sigmoid neuron의 output을 어떻게 해석해야 할까? perceptron과 sigmoid neuron의 가장 큰 변화는 sigmoid neuron은 0 또는 1 이외의 output을 가질 수 있다는 점이다. 0과 1 사이의 어떠한 실수가 될 수 있기 때문에 0.173과 0.689 와 같은 값들이 output이 될 수 있다. 이러한 속성은 매우 유용한데, 예를 들면 우리가 한 이미지 안에 있는 픽셀들의 평균 intensity를 neural network의 output으로 나타낼 수 있다는 점이다. 하지만 이러한 속성은 때때로는 매우 성가실 때도 있다. 만약 우리가 "이미지가 9다" 또는 "이미지가 9가 아니다" 이렇게 두가를 output으로 가지는 network가 있다고 가정해 보자. 이러한 경우에는 당연히 output을 0과 1로 표현하는 것이 훨씬 쉬울것이다. 하지만 output을 0.5보다 크거나 같은지에 따라 "9"인지 "9"가 아닌지를 결정하게 된다면 쉽게 문제를 해결할 수 있다.

Excercises

Sigmoid neuron simulating perceptrons, part 1

perceptron의 모든 weight와 bias를 양의 상수 $c > 0$로 곱했을때, network의 행동이 변하지 않는다는 것을 증명해라
Sigmoid neuron simulating perceptrons, part 2

???

The architecture of neural networks

다음 섹션에서 나는 손글씨 숫자들을 비교적 잘 분류하는 neural network를 소개할 것이다. 하지만 그 전에, 하나의 network에서의 부분들을 부르는 용어에 대해 설명하고자 한다. 다음과 같은 네트워크가 있다고 생각해 보자:

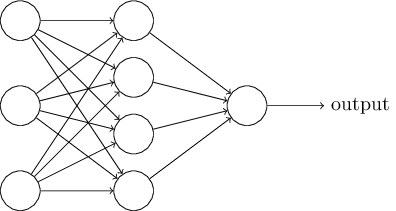
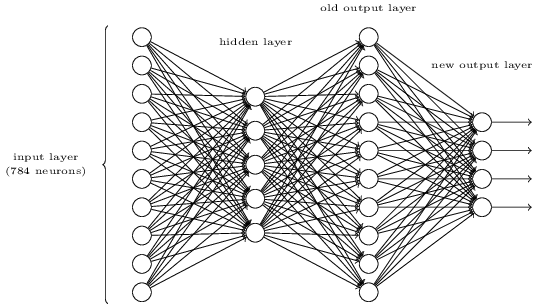
앞서 언급했다시피, 가장 왼쪽에 있는 layer를 $input layer$라고 부르고, 이 layer 안에 있는 neuron들을 $input neruon$이라 부른다. 가장 오른쪽 layer, 즉 $output layer$는 output neuron을 가진다(여기서는 하나의 output neuron만을 갖고 있다). 중앙에 있는 layer는 input 혹은 output layer도 아니기 때문에 $hiden layer$라고 부른다. 여기서 "hidden"이라는 단어가 조금 신비스럽게 들릴지도 모르지만 (처음에 내가 이 단어를 들었을때는 철학적인 혹은 수학적인 의미를 갖고 있다고 생각했다) 이 단어는 단지 "input도 output도 아닌"을 의마할 뿐이다. 위에 보이는 network는 하나의 hidden layer만 있지만, 여러개의 hidden layer를 가질수 도 있다. 예를 들면 아래의 4개의 layer를 가진 networt(four-layer network)는 두 개의 hidden layer를 갖고 있다.

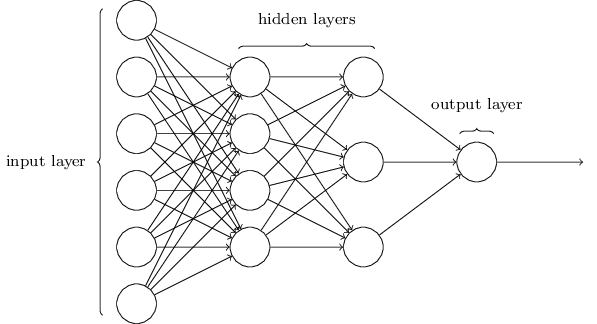
다소 혼란스럽겠지만 전통적인 이유로 위와 같은 sigmoid neuron으로 구성된 network를 multilayer percetpron 혹은 MLP라고 부른다. 하지만, 혼란을 막기위해 이 책에서 MLP라는 용어를 쓰지 않겠지만, 이러한 용어가 있다는 사실을 알려주고 싶다.

input과 output layer의 디자인은 가끔 쉬워보일때가 있다. 예를들면, 손글씨 숫자를 "9"인지 아닌지를 구분하고 싶다고 가정해 보자. 가장 자연스러워 보이는 방법은, 이미지 픽셀의 조명도를 input neuron으로 가지는 network를 만드는 것이다. 만약 이미지가 $64 \times 64$ 그레이스케일(greyscale) 이미지라면, $4,096 = 64 \times 64$개의 input neuron이 필요하다. 여기서 조명도는 0과 1 사이로 scale한 숫자들이 될 것이다. output layer에는 하나의 neuron만 있을것이고, output 값이 0.5보다 작으면 "input 이미지는 9가 아니다"라는 결론이 나오고, 0.5보다 크다면 "input 이미지는 9다"라는 결론이 나올것이다.

이렇게 input과 output layer를 디자인 하는 방법은 다소 쉬워 보이는 반면, hidden layer를 디자인 하는것은 꽤나 어려워 보인다. 특히, 몇개의 주먹구구식 경험들로 만든 규칙으로 hidden layer를 전체적으로 디자인하는것은 불가능하다. 그래서 nueral network 연구자들은 우리가 원하는 network를 얻을 수 있도록 도와주는 hideen layer 디자인을 위한 design heuristic을 많이 개발했다. 예를 들면, network를 트레이닝 하는데 드는 시간과 hidden layer의 갯수를 여떻게 trade off 할지에 대한 heuristic 방법론들이 있다. 그러한 design heuristic은 이후에 좀더 다뤄볼 예정이다.

지금까지 우리는 한 layer의 output이 다음 layer의 input으로 사용되는 neural network에 대해 다뤄왔다. 이러한 network를 우리는 *feedforward* (실행 전에 결함을 예측하고 행하는 피드백 과정의 제어) neural network라고 부른다. 이 말은 정보가 앞쪽 방향으로만 전달되고 반대 방향으로는 전달되지 않는, 다시 말하면 loop가 존재하지 않는 network를 의미한다. 만약 loop가 존재한다면 $\sigma$ 함수의 input이 output에 영향을 받는 상황이 생길 것이다. 그러한 상황은 말이 되지 않기 때문에 우리는 그러한 loop를 허용하지 않는다.

하지만, 다른 인공 신경 네트워크(artificial neural network) 모델에서는 feedback loop가 가능한 경우도 있다. 이러한 모델을 우리는 recurrent neural networks 라고 부른다.

A simple network to classify handwritten digits

지금까지 우리는 neural network를 정의했으며, 다시 손글씨 인지 문제로 돌아와 보자. 우리는 손글씨 인지 문제를 두개의 소문제(sub-problem)로 나눌 수 있다. 먼저, 우리는 이미지를 하나의 숫자만 포함하는 작은 이미지들로 나누는 것이다. 예를들어, 아래의 이미지를

6개의 분리된 이미지로 나누면,

위의 그림처럼 될 것이다. 우리 인간은 이러한 분할 문제 (segmentation problem) 을 손쉽게 해결할 수 있지만, 컴퓨터 프로그램에게는 그렇지 않다. 일단 이미지가 분리되고 나면, 프로그램은 각각의 숫자를 인지해야 한다. 위의 예시에서 처음으로 분할된 이미지를

프로그램은 5라고 인지해야 할 것이다.

우리는 두번째 문제, 즉 각각의 숫자를 분류하는 문제를 해결하는 프로그램을 짜는데 집중할 것이다. 왜냐하면 여러분이 하나의 숫자를 구분할 수 있다면, 분할 문제를 해결하는 것은 크게 어렵지 않기 때문이다. 이미지 분할 문제를 해결하는 방법에는 여러가지가 있다. 한가지 방법으로는 여러번 이미지를 나눠 본 후 시도한 분할을 단일 숫자 분류기로 점수를 내는 것이다. 만약 단일 숫자 분류기가 작은 이미지들을 분류하는데 어려움을 겪지 않았다면 높은 점수를 받을 것이고, 숫자를 인지하는데 어려움을 겪는다면 낮은 점수를 받을것이다. 이 방법의 핵심 아이디어는, 만약 단일 숫자 분류기가 어딘가에서 난항을 겪는다면, 아마 이미지 분할이 제대로 이루어지지 않았을 가능성이 높다는 데에 있다. 이러한 아이디어 뿐만 아니라 다른 여러가지 방법으로 이미지 분할 문제를 잘 해결할 수 있을 것이다. 그렇기 때문에, 이미지 분할 문제 보다는 더 흥미롭고 어려운 단일 숫자를 분류할 수 있는 neural network를 만드는 데에 집중할 것이다.

하나의 숫자를 인지하기 위해 다음과 같은 3개의 layer를 가진 neural network를 이용할 것이다:

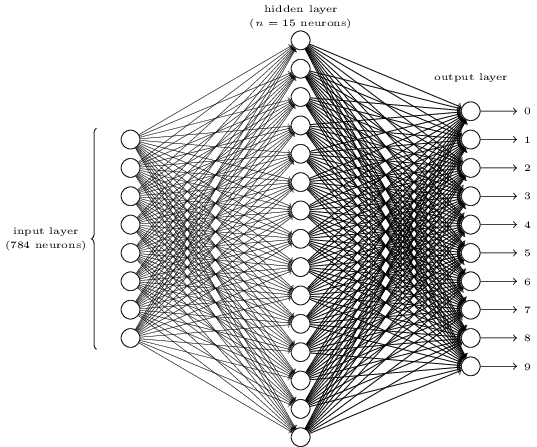
input layer는 픽셀들의 값을 인코딩한 뉴런들로 구성되어 있다. 다음 섹션에서 다루겠지만, 우리의 training data는 $28 times 28$ 픽셀 이미지기 때문에 $784 = 28 times 28$개 만큼의 neuron을 필요로 한다. 간단하게 그리기 위해서 위의 그림에서는 neuron을 많이 생략했다. input pixel은 흰색을 의미하는 0.0 부터 검정색을 의미하는 1.0 까지의 실수 값을 가지게 되며, 그 값은 회색의 진한 정도를 나타낸다.

두번째 layer는 hidden layer다. hidden layer에 존재하는 neuron의 갯수를 $n$으로 나타내며 우리는 $n$을 바꿔가며 실험을 진행할 것이다. 위의 예시에 나와있는 hidden layer는 $n = 15$개의 neuron을 갖고 있다.

output layer는 10개의 neuron을 갖고 있다. 만약 첫번째 neuron의 상태가 output $\approx 1$이면 network가 input 이미지를 0으로 인식한다는 것을 의미한다. 만약 두번째 neuron의 상태가 $\approx 1$이면 이미지를 1로 인식한다는 것이다. 좀더 정확하게 설명하면, 우리는 output neuron을 0 부터 9까지 숫자를 붙이고, 어떤 neuron이 가장 높은 activation 값을 가지고 있는지 알아낼 것이다. 만약 6이라고 이름 붙인 neuron의 값이 가장 크다면, network는 input 숫자를 6으로 인지하고 있다는 의미다.

당신은 아마 왜 우리가 10개의 output neuron을 사용하고 있는지 궁금할 것이다. 그 이유는 우리가 만들고 있는 netork가 숫자 0, 1, 2, ... , 9를 구분해야하기 때문이다. 하지만 여러분은 각각의 output을 이진수로 생각해서, 4개의 output neuron으로도 충분하다고 생각할 지도 모른다. 이렇게 생각하는 이유는, $2^4 = 16$이기 때문에 충분히 10개의 가능한 값을 구분할 수 있을 것이라 말하고 싶을것이다. 하지만 왜 우리는 10개의 neuron을 상용해야만 하는 것일까? 그것은 비효율적이지 않을까? 우리가 이를 정당화 할 수 있는 방법은 경험에 의거했기 때문이다. 우리는 두가지 network를 모두 만들어 실험을 해 보았지만, 10개의 neuron을 가진 network가 4개의 neuron을 가진 network 보다 숫자를 더 잘 인지했다. 이런 경험적 증명이 아닌 다른 방법으로 10개 output network가 4개 output neuron보다 뛰어난 이유를 설명할 수 있을까?

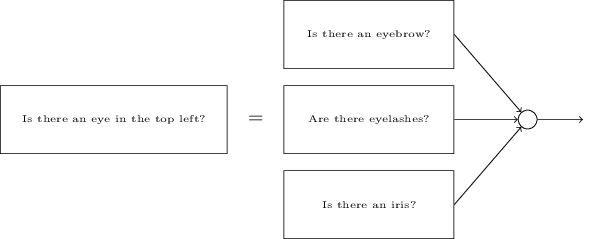
이것을 이해하기 위해서, 처음으로 돌아가 neural network가 무엇인지에 대해 생각해 보는것이 도움이 된다. 먼저 10개 output neuron의 경우를 보자. 첫번째 output neroun을 보면, 이것은 input 이미지의 숫자가 0인지 아닌지를 hidden layer를 거치면서 결정된다. 그렇다면 hidden neroun들은 무엇을 하는 것일까? 여기서 hidden layer의 첫번째 neroun이 아래와 같은 이미지가 있는지 없는지를 알아낸다고 가정해 보자:

그렇다면, input 이미지와 위의 이미지를 겹쳐서 겹친 부분의 pixel에는 큰 weight를 곱하고, 그렇지 않은 pixel에는 작은 weight를 곱하면 될 것이다. 비슷한 방식으로, hhidden layer의 두번째, 세번째 그리고 네번째 neuron은 아래에 나열된 이미지가 존재하는지 존재하지 않는지를 구분한다고 가정해 보자:

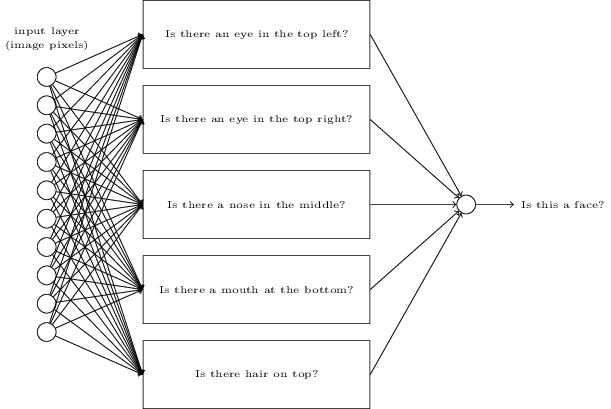
위에 그림들을 조합해 보면, 각각의 이미지가 0의 부분 이미지라는 것을 알 수 있을것이다:

그래서 위에서 언급된 4개의 hidden neuron이 active라면 우리는 숫자가 0이라고 결론을 내릴 수 있을 것이다. 하지만 당연히 이 방법만이 숫자 0을 결정하는 증거가 되는 것은 아니다. 예를 들면, 앞서 제시한 4개의 이미지를 조금씩 변형할 수도 있고, 찌그러 트릴 수도 있다. 어쨋든, 적어도 이 방법으로 0을 안전하게 인지할 수 있을것으로 보인다.

이러한 방법으로 network 함수들을 생각해 본다면, 우리는 왜 4개의 경우보다 10개의 output을 가진 network의 성능이 더 높다는 것을 그럴듯 하게 설명할 수 있을 것이다. 만약 4개의 output neuron의 경우를 상상해 본다면, 쉽게 위와 같은 process를 상상하기 어려울 것이다.

하지만 결론적으로 이것은 모두 경험적 실험에 의한 결과이다. 그 어떤것도 3개 layer의 neural network가 내가 설명한 것처럼 작동할 것이라는 걸 증명하지 않는다. 아마 좀더 똑똑한 learning algorithm을 사용한다면 4개의 output neuron의 경우에 적합한 wiehgt를 찾아낼 지도 모른다. 하지만, 나의 실험적 결과로는 10개의 output neuron의 경우가 훨씬 더 잘 작동했고, 이 사실은 여러분이 neural network 구조를 디자인하는데 있어 많은 시간을 줄여 줄 것이다.

Learning with gradient descent

이제 우리에겐 neural network의 전체적인 디자인이 있다. 그런데 어떻게 이 network>가 숫자를 인지하는 것을 배울 수 있을까? 가장 먼저, 우리에게 필요한 것은 "training dataset"이라고 불리는 숫자 인지를 배울 데이터가 필요하다. 우리는 수만개의 손글 씨 숫자 이미지를 스캔한 이미지와 그 이미지에 해당하는 숫자가 있는 MNIST 데이터 셋 을 사용할 것이다. MNIST라는 이름은 NIST (the United States' National Institute of Standards and Technology)에 의해 모>여진 데이터를 수정한 부분 데이터이기 때문에 붙여졌다. 아래는 MNIST 에 포함된 몇>개의 이미지 예시다:

사실 이미지는 이 챕터를 시작할 때 보여줬던 이미지들이다. 당연히 우리의 network를

테스트 할 때에는 training set에서 사용했던 이미지들은 사용하지 않을 것이다!

MNIST 데이터는 두개의 부분으로 나뉜다. 첫번째 파트는 60,000개의 이미지로 구성되>어 있고 training data로 사용할 것이다. 이 이미지들은 250명의 사람들로부터 얻은 >스캔한 손글씨들이며, 반은 US Census Bureau 노동자들로부터, 나머지 반은 고등학교 학생들로부터 얻었다. 이미지들은 28 * 28 픽셀 사이즈로 회색톤(greyscale)으로 되어 있다. MNIST의 두번째 파트는

여기서 우리가 원하는 것은 모든 training input $x$에 대해서 network의 output이 $y(x)$와 근접한 결과를 만들어내는 weight와 bias를 찾는 알고리즘이다. 얼마나 우리가 목표와 근접한지를 계산하기 위해 우리는 cost function을 다음과 같이 정의한다:

\begin{eqnarray} C(w,b) \equiv \frac{1}{2} \sum_x \| y(x) - a\|^2. \tag{6}\end{eqnarray}

여기서 $w$는 network의 모든 weight를 나타내고, b는 bias를, a는 x라는 input에 대해 계산한 network의 output값을 의미한며, 모든 training input인 x에 대한 식의 합을 계산한다. 당연히, output a는 x, w, b에 의존적이지만, 이 식을 간단하게 표현하기 위해 나는 이런 의존성을 명확히 표시하지는 않았다. 여기서 cost function을 $C$로 표현하고 quadratic cost function이라 부른다. 또한 이 식은 mean squred error, 즉 MSE라고 표현되기도 한다. quatratic cost function을 잘 들여다 보면, $C(w,b)$가 양수 값의 합이기 때문에 결과적으로 양수가 된다는 것을 알 수 있다. 그리고, 모든 training input $x$에 대해 $y(x)$가 output $a$에 근접한다면 $C(w,b)$는 작아지고, $C(w,b) \approx 0$가 될 것이다. 그렇기 때문에 우리의 training 알고리즘이 $C(w,b) \approx 0$를 만드는 적절한 weight와 bias를 찾는다면 좋은 알고리즘이라고 볼 수 있겠다. 하지만 반대로, 많은 input $x$에 대해 $y(x)$가 output $a$에 근접하지 않는다면 $C(w,b)$는 결국 큰 숫자가 될 것이고, 이러한 weight와 bias를 찾는 알고리즘은 좋은 알고리즘이 아니다. 그래서 weight와 bias의 함수인 $C(w,b)$를 최소화하는 training 알고리즘을 찾는것이 우리읭 목표이다. 다시 말하자면, cost를 가장 작게 만드는 weight와 bias를 찾아야 한다는 것이다. 여기서 우리는 gradient descent라고 알려진 algorithm을 사용할 것이다.

그렇다면 왜 quadratic cost를 소개했을까? 결국 우리가 진짜로 관심있는 것은 적절하게 이미지를 분류하는 network 아닌가? quadratic cost와 같은 측정법을 최소화 하는 대신, 숫자를 정확하게 예측하는 정도를 최대화 하려고 하지 않을까? 여기서 문제는 정확히 분류된 이미지의 "수"는 weight와 bias의 부드러운 함수(smooth function) 형태를 만들기 어렵다. 대부분의 경우 weight와 bias를 조금 바꾸는 것으로는 정확히 분류된 training 이미지의 "수"에는 큰 변화를 주지 않는디. 그렇기 때문에 이런 방식으로는 어떻게 weight와 bias를 바꿔야 성능이 좋아지는지를 알아내기 힘들다. 그 대신에 우리가 quadratic cost와 같은 cost 함수를 사용한다면 cost를 줄이기 위해서 어떻게 wieght와 bias를 바꿔야 하는지 쉽게 알아낼 수 있을것이다. 그렇기 때문에 우리는 먼저 quadratic cost를 줄이는데 집중을 하고, 그 후에 분류의 정확도를 조사할 것이다.

이제 당신은 왜 cost function을 사용해야 하는지 알았더라도, 여전히 왜 quadratic function을 사용했는지 궁금해 할 수 있다. quadratic function 말고는 다른 옵션은 없을까? 만약 우리가 다른 cost function을 사용한다면 완전히 다른 weight와 bias를 얻게 되지는 않을까? 이러한 고민을 하는것은 당연하며, 나중에 우리는 다른 cost function을 사용해 볼 것이다. 하지만, quadratic cost function은 neural network를 이해하는데 매우 적합한 함수이기 때문에 당분간은 이것을 사용할 것이다.

다시 정리하자면, neural network를 training하는데 있어 우리의 목표는 quadratic cost function인 $C(w,b)$를 최소화 하는 것이다.

이제 우리에겐 neural network의 전체적인 디자인이 있다. 그런데 어떻게 이 network가 숫자를 인지하는 것을 배울 수 있을까? 가장 먼저, 우리에게 필요한 것은 "training dataset"이라고 불리는 숫자 인지를 배울 데이터가 필요하다. 우리는 수만개의 손글씨 숫자 이미지를 스캔한 이미지와 그 이미지에 해당하는 숫자가 있는 MNIST 데이터 셋 을 사용할 것이다. MNIST라는 이름은 NIST (the United States' National Institute of Standards and Technology)에 의해 모여진 데이터를 수정한 부분 데이터이기 때문에 붙여졌다. 아래는 MNIST 에 포함된 몇개의 이미지 예시다:

사실 이미지는 이 챕터를 시작할 때 보여줬던 이미지들이다. 당연히 우리의 network를 테스트 할 때에는 training set에서 사용했던 이미지들은 사용하지 않을 것이다!

MNIST 데이터는 두개의 부분으로 나뉜다. 첫번째 파트는 60,000개의 이미지로 구성되어 있고 training data로 사용할 것이다. 이 이미지들은 250명의 사람들로부터 얻은 스캔한 손글씨들이며, 반은 US Census Bureau 노동자들로부터, 나머지 반은 고등학교 학생들로부터 얻었다. 이미지들은 28 * 28 픽셀 사이즈로 회색톤(greyscale)으로 되어있다. MNIST의 두번째 파트는

( .. 진행중 .. )

[번역] Neural Network를 이용한 손글씨 인지